6.3.2 Paxos 算法
希望你没有对前篇 Paxos 的“复杂”做的铺垫所吓倒,共识问题已经算是一个古老的领域,30 余年间已经有无数简洁直白的视频、论文等资料进行过解读[1]。接下来,我们先了解 Paxos 基本背景,然后直面 Paxos 算法细节,最后用具体的例子验证 Paxos 算法。
1. Paxos 算法背景
在 Paxos 算法中,节点分为三种角色。
- 提议者(Proposer):提议者是启动共识过程的节点,它提出一个值,请求其他节点对这个值进行投票,提出值的行为称为发起“提案"(Proposal),提案包含提案编号 (Proposal ID) 和提议的值 (Value)。注意的是,Paxos 算法是一个典型的为“操作转移”模型设计的算法,为简化表述,本文把提案类比成“变量赋值”操作,但你应该理解它是“操作日志”相似的概念,后面介绍的 Raft 算法中,直接就把“提案”称做“日志”了。
- 决策者(Acceptor):接受或拒绝提议者发起的提案,如果一个提案被超过半数的决策者接受,意味着提案被“批准”(accepted)。提案一旦被批准,意味着在所有节点中达到共识,便不可改变、永久生效。
- 记录者(Learner):记录者不发起提案,也不参与决策提案,它们学习、记录被批准的提案。
在 Paxos 算法中,所有节点都是平等的,能够承担一种或多种角色。例如,提议者既可以发起提案,也可以对其他提案进行表决。但为了更明确地计算 Quorum,通常建议表决提案的节点数为奇数。
在 Paxos 算法中,所有节点都可以发起提案。如果两个节点同时发起提案,就会导致提案冲突。如图 6-5 所示,S1 向 S1、S2、S3 发起提案(red)。同时,S5 也向 S3、S4、S5 发起提案(blue)。它们的提案 Quorum 都达成了,也就是说一个提案有两个值被批准,这显然破坏了一致性原则。

图 6-5 网络延迟导致冲突
根据图 6-5,你会发现提案冲突发生在 S3,S3 是两个 Quorum 的交集点,它的时间线上有两个不同的值被批准。
我们知道,设计程序的一个基本常识是,如果多个线程同时操作某个共享变量,一定要加上互斥锁,不然会出现各种意外情况。不难发现,S3 问题的本质是“在分布式环境下并发操作共享变量的问题”。
由于分布式环境中随时可能发生通信故障,我们不能粗暴“套用”进程加锁机制来解决 S3 的问题。举个例子,如果一个节点在获得锁后故障,且在释放锁之前发生故障,整个系统可能会陷入无限期的阻塞状态。
解决上述问题的关键在于,得有一种可供其他节点抢占锁的机制,避免因通信故障导致死锁。
在本书第五章第 5.2 节中,笔者介绍了“乐观锁”。分布式抢占锁的设计思想与“乐观锁”有异曲同工之妙。回顾乐观锁的示例 SQL,WHERE 条件用于判断在操作之前数据是否已被修改。如果数据已被修改,则请求最新的数据,更新版本号,并通过重试机制再次进行修改。
UPDATE accounts
SET balance = balance + ?,
version = version + 1
WHERE id = ? AND version = ?;
我们可以借鉴“乐观锁”的思路,尝试解决图 6-5 所示的冲突问题。
首先,S1 发起提案,S3 收到 S1 提案时,应该意识到 S5 发起的提案(blue)的 Quorum 已经达成,S1 提案(red)已经失效。根据先到先得原则,S1 应该更新自己的提案值(red 替换为 blue),这个操作相当于对提案编号(乐观锁中的 version)“锁定”,防止之后出现多个冲突的提案编号。
一旦了解了哪些提案被接受,接下来的处理就变得简单了。现在,我们可以直面 Paxos 算法的细节了。
2. Paxos 算法描述
简而言之,Paxos 算法本质是一个支持多次重复的二阶段提交协议。
Paxos 算法的第一个阶段称“准备阶段”(Prepare)。提议者选择一个提案编号 (通常是单调递增的数字,相当于乐观锁中的 version,更高的编号意味着更高的优先级),向所有的决策者广播许可申请(称为 请求),如果决策者:
- 尚未承诺 编号的提案:则“承诺”(promise)不再接受任何编号小于 的提案,返回一个响应,其中包含承诺的提案编号以及对应的提案值(如果有);
- 已承诺 编号的提案:拒绝 Prepare 请求,不返回任何响应。
提议者从多数决策者获得了“承诺”(Promise),则“准备阶段”达成。接着,决策者选择提案值:如果决策者的响应中返回了提案值,从中选择编号最高的提案值;如果没有提案值返回,则使用决策者初始提案值。
完成以上操作后,进入下一个阶段。
Paxos 算法的第二个阶段称“批准阶段”(Accept)。提议者向所有决策者广播批准申请(称为 请求),请求批准:“提案编号 提案值 ”。如果决策者发现提案编号 不小于它已承诺的最大编号,则“批准”(accepted)该提案;否则拒绝该提案。当多数的决策者批准提案时,提议者认为本轮提案成功、共识达成。一旦提案成功,提议者会将最终的决议广播给所有记录者节点,供它们学习、记录最终结果。
图 6-6 Paxos 算法流程
3. Paxos 算法验证
证明 Paxos 算法的正确性比重新实现 Paxos 算法还难。我们没必须推导 Paxos 的正确性,通过以下几个例子来验证 Paxos 算法。
下面的示例中,X、Y 代表客户端,S1 ~ S5 是服务端,它们既是提议者又是决策者,图中的 P 代表 “准备阶段”,A 代表“批准阶段”。为了便于理解,提案编号 由自增序号和 Server ID 组成。例如,S1 的提案编号为 1.1、2.1、3.1...。
现在,我们来分析 S1 、S5 同时发起提案,会出现什么情况。
情况一:提案已批准。如图 6-7 所示,S1 收到客户端的请求,于是 S1 作为提议者,向 S1...S3 广播 Prepare(3.1) 消息,决策者 S1...S3 没有接受过任何提案,所以接受该提案。接着,S1 广播 Accept(3.1, X) 消息,提案 X 成功被批准。
在提案 X 被批准后,S5 收到客户端的提案 Y,S5 作为提议者向 S3...S5 广播 Prepare(4.5) 消息。对 S3 来说,4.5 比 3.1 大,且已经接受了 X,它回复提案 (3.1, X)。S5 收到 S3...S5 的回复后,使用 X 替换自己的 Y,接着进入批准阶段,广播 Accept(4.5, X) 消息。S3...S5 批准提案,所有决策者就 X 达成一致。

图 6-7 提案已批准
情况二:事实上,对于情况一,也就是“取值为 X”并不是一定需要多数派批准,S5 发起提案时,准备阶段的应答中是否包含了批准过 X 的决策者也影响决策。如图 6-8 所示,S3 接受了提案 (3.1, X),但 S1、S2 还没有收到 Accept(3.1, X) 消息。此时 S3、S4、S5 收到 Prepare(4.5) 消息,S3 回复已经接受的提案 (3.1, X),S5 将提案值 Y 替换成 X,广播 Accept(4.5, X) 消息给 S3、S4、S5,对 S3 来说,编号 4.5 大于 3.1,所以批准提案 X,最终共识的结果仍然是 X。
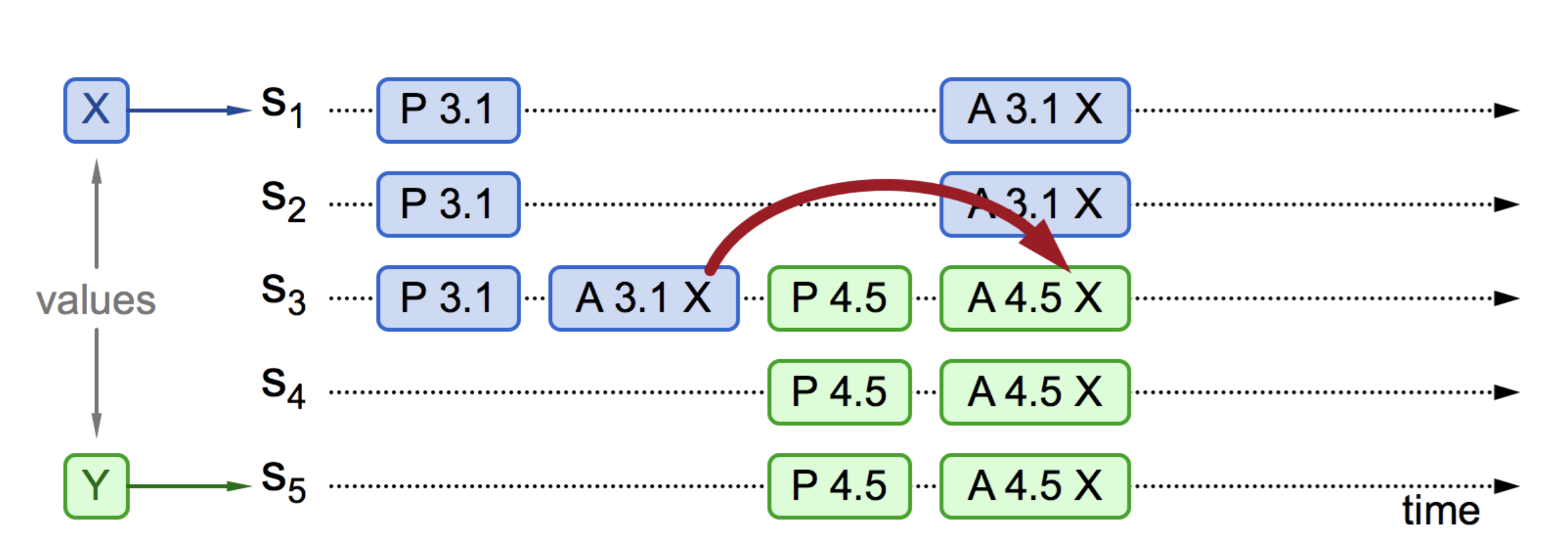
图 6-8 提案部分接受,新提议者可见
情况三:另外一种可能的情况是 S5 发起提案时,准备阶段的应答中未包含批准过 X 的决策节点。S1 接受了提案 (3.1, X),S3 先收到 Prepare(4.5) 消息,后收到 Accept(3.1, X) 消息,由于 3.1 小于 4.5,会直接拒绝这个提案。提案 X 没有收到多数的回复,X 提案就被阻止了。提案 Y 顺利通过,整个系统最终对“取值为 Y”达成一致。
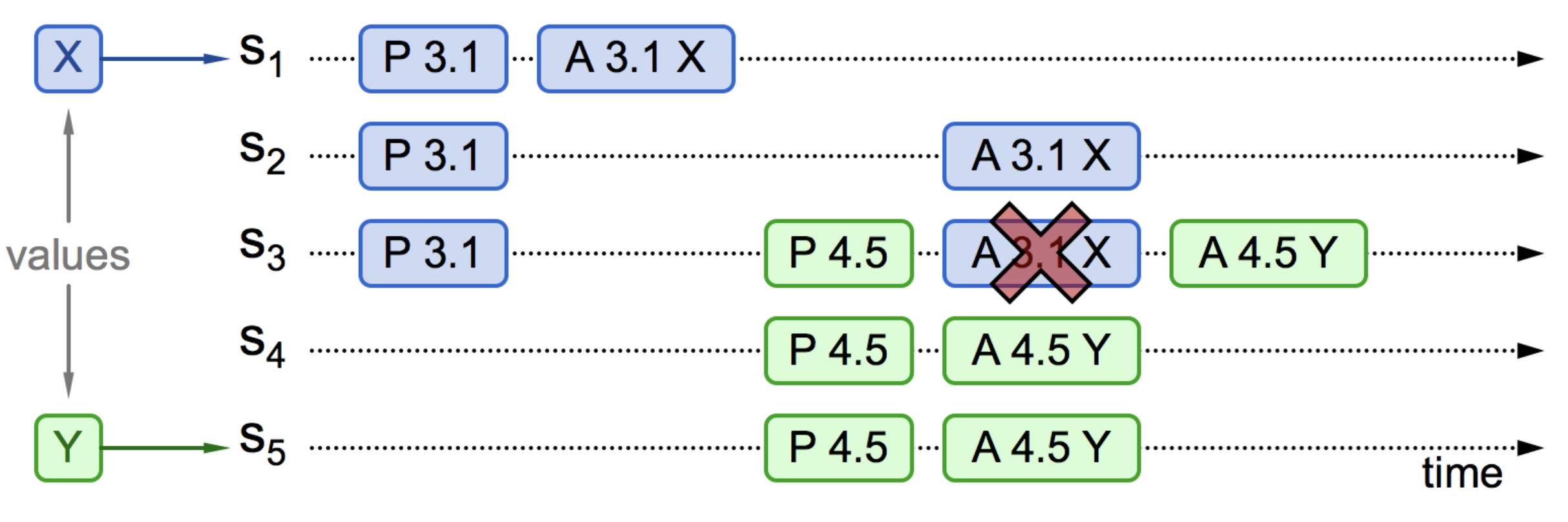
图 6-9 提案部分接受,新提议者不可见
情况四:从情况三可以推导出另一种极端的情况,多个提议者同时发起提案,在准备阶段互相抢占,反复刷新决策者上的提案编号,导致任何一方都无法达到多数派决议,这个过程理论上可以无限持续下去,形成“活锁”(livelock)。
解决这个问题并不复杂,将重试时间随机化,就能减少这种巧合发生。
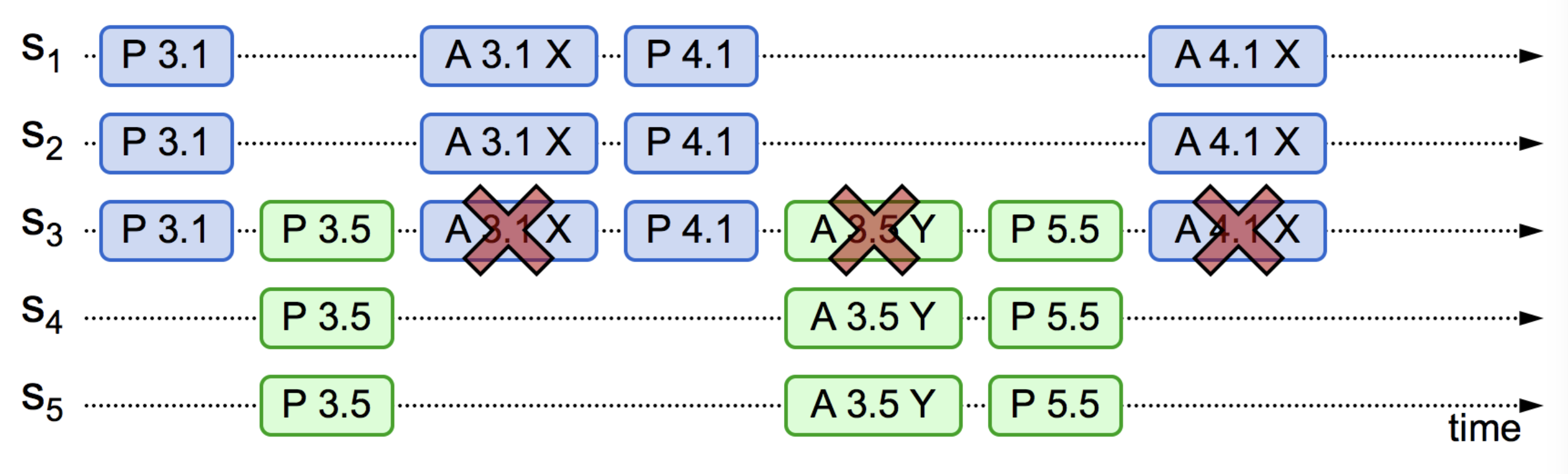
图 6-10 出现活锁问题
以上,就是整个 Paxos 算法的工作原理。
Paxos 算法只能处理单个提案,达成共识至少需要两次网络往返,高并发情况下还可能导致活锁。因此,Paxos 算法主要用于理论研究,很少直接用于工程实践。后来,Lamport 在论文《Paxos Made Simple》中提出了 Paxos 的变体 —— Multi Paxos。Multi Paxos 引入了“选主”机制,通过多轮运行 Paxos 算法来处理多个提案。
不过,Lamport 的论文主要聚焦于 Paxos 正确性证明,对于领导者选举、多轮提案并没有给出实现细节。2014 年,斯坦福的学者 Diego Ongaro 和 John Ousterhout 发表了论文《In Search of an Understandable Consensus Algorithm》,该论文基于 Multi Paxos 思想,提出了“选主”、“日志复制”的概念,并给出了详细的实现细节。该论文斩获 USENIX ATC 2014 大会 Best Paper 荣誉,更是成为后来 etcd、Consul 等分布式系统的实现基础。
讲解作者是斯坦福教授 John Ousterhunt,他还指导了 Diego Ongaro 写出了 Raft 的论文。本章配图也多来源于 John Ousterhunt 所发表的内容。 ↩︎